主成分分析、Principal component analysis (PCA)
loadingsパッケージを用いた主成分分析の流れについて説明する.
- データの説明
- loadingsパッケージのデモデータfastingを利用する
- 通常飼育と12時間絶食後のマウスの肝臓のメタボロームデータ(各群n=5)
ライブラリとデータの読み込み
はじめに,loadingsパッケージのデモデータfastingを読み込む.実際の解析の場合は,csvファイルをread.csv関数などでデータを読み込んで利用する.
fastingの変数Xに,各行にサンプル,各列に代謝物のメタボロームデータが含まれている.
次に,主成分分析を行う.主成分分析はprcomp関数を用いる.ここではデータをautoscaling(各代謝物毎に,平均0,分散1にする) によるスケーリングを行っている.
pca <- prcomp(X,scale=TRUE) # PCA with autoscaling
PC_score <- pca$x[,c(1,2)] # First and second PC score
# PC score plot
class <- c(1,1,1,1,1,2,2,2,2,2)
plot(PC_score, col=class, pch=16, cex=2)
主成分分析の結果より,第1主成分で群間差が確認されたことから,第1主成分スコアと関連する代謝物を確認することで,12時間の絶食で低値もしくは高値を示す代謝物を確認することが出来る.
PC_weight <- pca$rotation # weight / PC coefficient / eigenvector
PC1_weight <- pca$rotation[,1] # PC1 weight
実際に,第1主成分スコアと関連する代謝物を主成分係数を用いて確認する.主成分係数の値が正または負に大きな上位10個の代謝物は次のようになる.
# top 10 metabolites (positively correlated)
PC1_weight[order(PC1_weight, decreasing=TRUE)[1:10]]## Ethanolamine phosphate 3-Aminobutyric acid
## 0.09225381 0.09122681
## Pyridoxal O-Succinylhomoserine
## 0.09079419 0.08883521
## 3-Hydroxybutyric acid Choline
## 0.08819795 0.08775669
## Adipic acid Carnitine
## 0.08766638 0.08746767
## Suberic acid N-Acetylglucosamine 6-phosphate
## 0.08578445 0.08566279
# top 10 metabolites (negatively correlated)
PC1_weight[order(PC1_weight, decreasing=FALSE)[1:10]]## Betonicine S-Lactoylglutathione
## -0.09214178 -0.09199026
## Glucose 1-phosphate Glucose 6-phosphate
## -0.09156145 -0.09153070
## Stachydrine Fructose 6-phosphate
## -0.09034003 -0.08966964
## Pyruvic acid GDP-mannose ; GDP-galactose
## -0.08958449 -0.08932628
## 5-Aminovaleric acid Lactic acid
## -0.08885122 -0.08882916主成分係数を用いて,主成分スコアと関連する代謝物を見つけることが出来るが, その値の大きさがどの程度であれば強く関連する代謝物と言えるのか,判断することが難しい.
主成分係数と主成分負荷量の関係
そこで,主成分係数の代わりに,「主成分スコアと各代謝物レベルの相関係数」である主成分負荷量を利用することを考える.
主成分係数と主成分負荷量の関係を確認するために,横軸に主成分係数,縦軸に主成分負荷量の散布図を以下に示す.
R <- NULL
for(i in 1:ncol(X)){
R[i] <- cor.test(PC_score[,1],X[,i])$estimate
}
plot(PC1_weight,R, xlab = "PC coefficient", ylab="PC loading")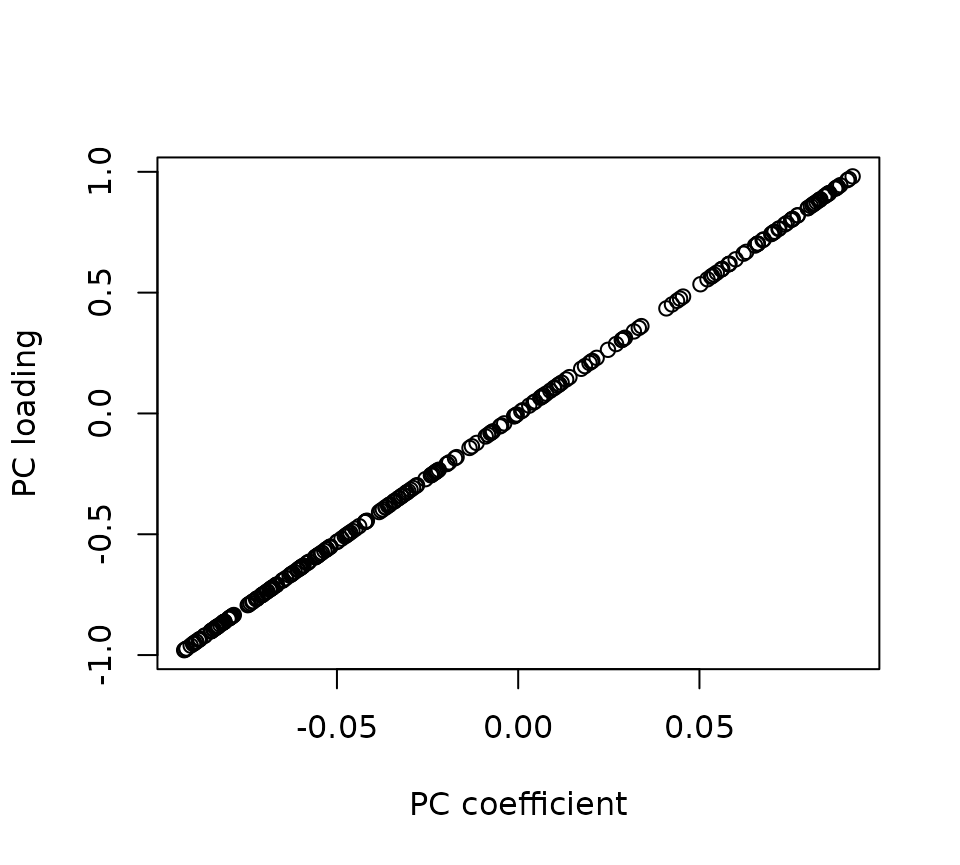
それに加えて,主成分負荷量は「主成分スコアと各代謝物レベルの相関係数」として定義されることから, 主成分負荷量を用いることで,例えば0.7以上で強い相関があるといった統計的な基準で代謝物を選ぶことが出来る.
主成分負荷量は,主成分スコアの分散の平方根(標準偏差)を主成分係数に掛けることで計算することが出来る.
loadingsパッケージを用いた主成分負荷量は,pca_loading関数を用いて,以下のように簡単に計算することが出来る.
pca <- pca_loading(pca)
PC_loading <- pca$loading$R
p <- pca$loading$p.valueまた主成分負荷量の統計的仮説検定により,p-valueを用いて有意な代謝物を選ぶことも出来る.[Yamamoto H. et al., BMC Bioinformatics, (2014) 15(1):51.]
主成分負荷量を用いて代謝物を選ぶ
実際に,第1主成分負荷量を用いて第1主成分スコアと関連する代謝物を選ぶと以下のようになる.
PC1_loading <- PC_loading[,1]
# top 10 metabolites (positively correlated)
PC1_loading[order(PC1_loading, decreasing=TRUE)[1:10]]## Ethanolamine phosphate 3-Aminobutyric acid
## 0.9810803 0.9701587
## Pyridoxal O-Succinylhomoserine
## 0.9655579 0.9447249
## 3-Hydroxybutyric acid Choline
## 0.9379480 0.9332554
## Adipic acid Carnitine
## 0.9322950 0.9301818
## Suberic acid N-Acetylglucosamine 6-phosphate
## 0.9122814 0.9109877
# top 10 metabolites (negatively correlated)
PC1_loading[order(PC1_loading, decreasing=FALSE)[1:10]]## Betonicine S-Lactoylglutathione
## -0.9798890 -0.9782776
## Glucose 1-phosphate Glucose 6-phosphate
## -0.9737174 -0.9733904
## Stachydrine Fructose 6-phosphate
## -0.9607281 -0.9535988
## Pyruvic acid GDP-mannose ; GDP-galactose
## -0.9526933 -0.9499474
## 5-Aminovaleric acid Lactic acid
## -0.9448953 -0.9446607さらに,第1主成分負荷量が0.7以上の代謝物は45物質,-0.7以下の代謝物70物質, p<0.05の代謝物は138物質,Benjamini-Hochberg法によるq-valueがq<0.05の代謝物は102物質であった.
# Number of positively correlated metabolties
sum(PC1_loading>=0.7)## [1] 45
# Number of negatively correlated metabolties
sum(PC1_loading<=-0.7)## [1] 70
# Statistical hypothesis testing of PC loading
p_PC1 <- pca$loading$p.value[,1]
# Number of significant metabolites under p<0.05
sum(p_PC1 < 0.05)## [1] 138## [1] 102最後に,第1主成分スコアと最も相関の高い代謝物は,それぞれEthanolamine phosphateとBetonicineであり, その値はそれぞれEthanolamine phosphate(R=0.981, p=5.48×10^-7, q=8.92×10^-5),Betonicine(R=-0.980, p=6.99×10^-7, q=8.92×10^-5)であった.
# Ethanolamine phosphate (top 1 positively correlated metabolite with PC1 score)
par(mfrow=c(1,2))
plot(PC_score[,1], col=class, pch=16, cex=2, xlab="Sample", ylab="PC1")
plot(X[,order(PC1_loading, decreasing=TRUE)[1]],col=class, pch=16, cex=2, xlab ="Sample", ylab="Ethanolamine phosphate")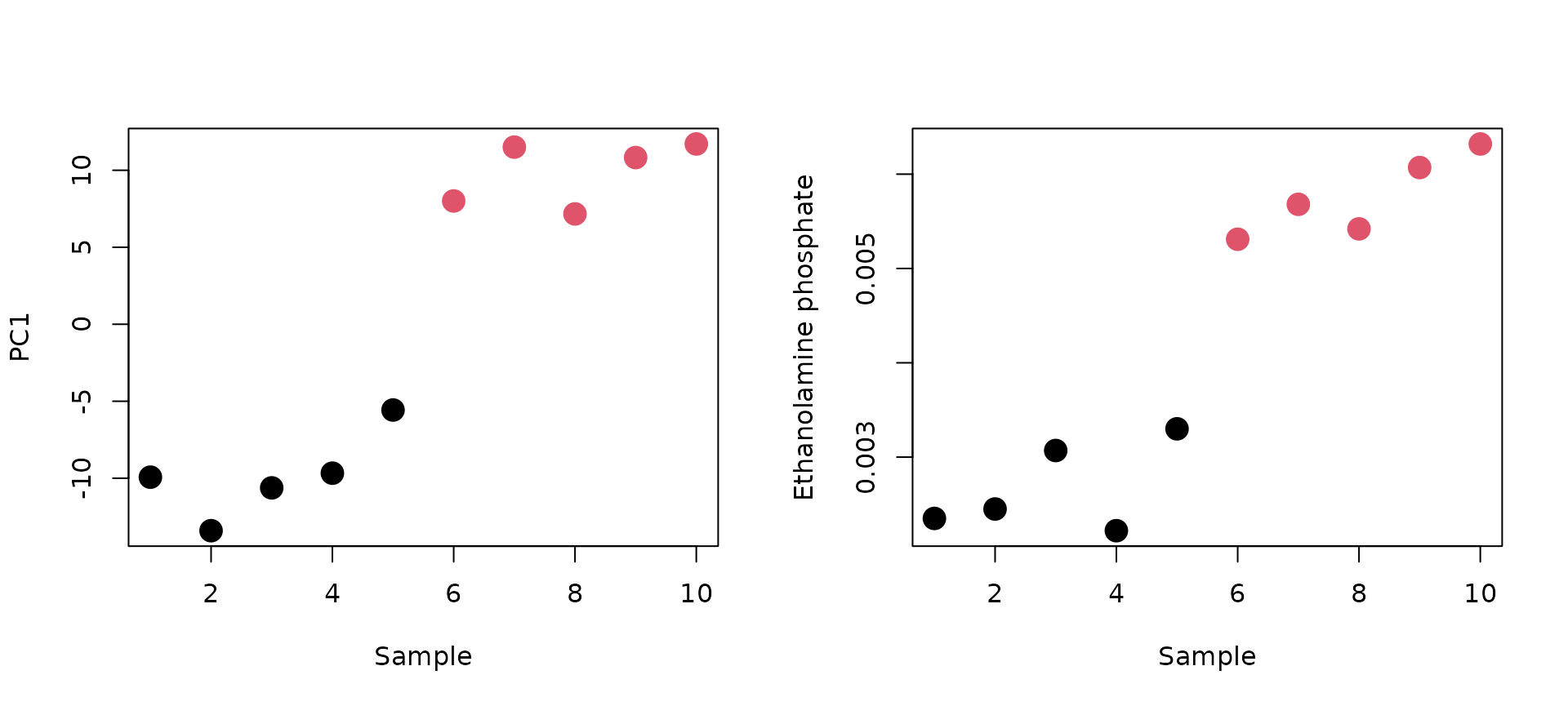
上図の左が第1主成分スコア,右がEthanolamine phosphateである(横軸はサンプル番号).主成分負荷量(相関係数)の値が0.981と非常に高い値を示すことから分かるように,非常に良く似た傾向を示すことが確認できる.
# Betonicine (top 1 negatively correlated metabolite with PC1 score)
par(mfrow=c(1,2))
plot(PC_score[,1], col=class, pch=16, cex=2, xlab="Sample", ylab="PC1")
plot(X[,order(PC1_loading, decreasing=FALSE)[1]],col=class, pch=16, cex=2,xlab ="Sample", ylab="Betonicine")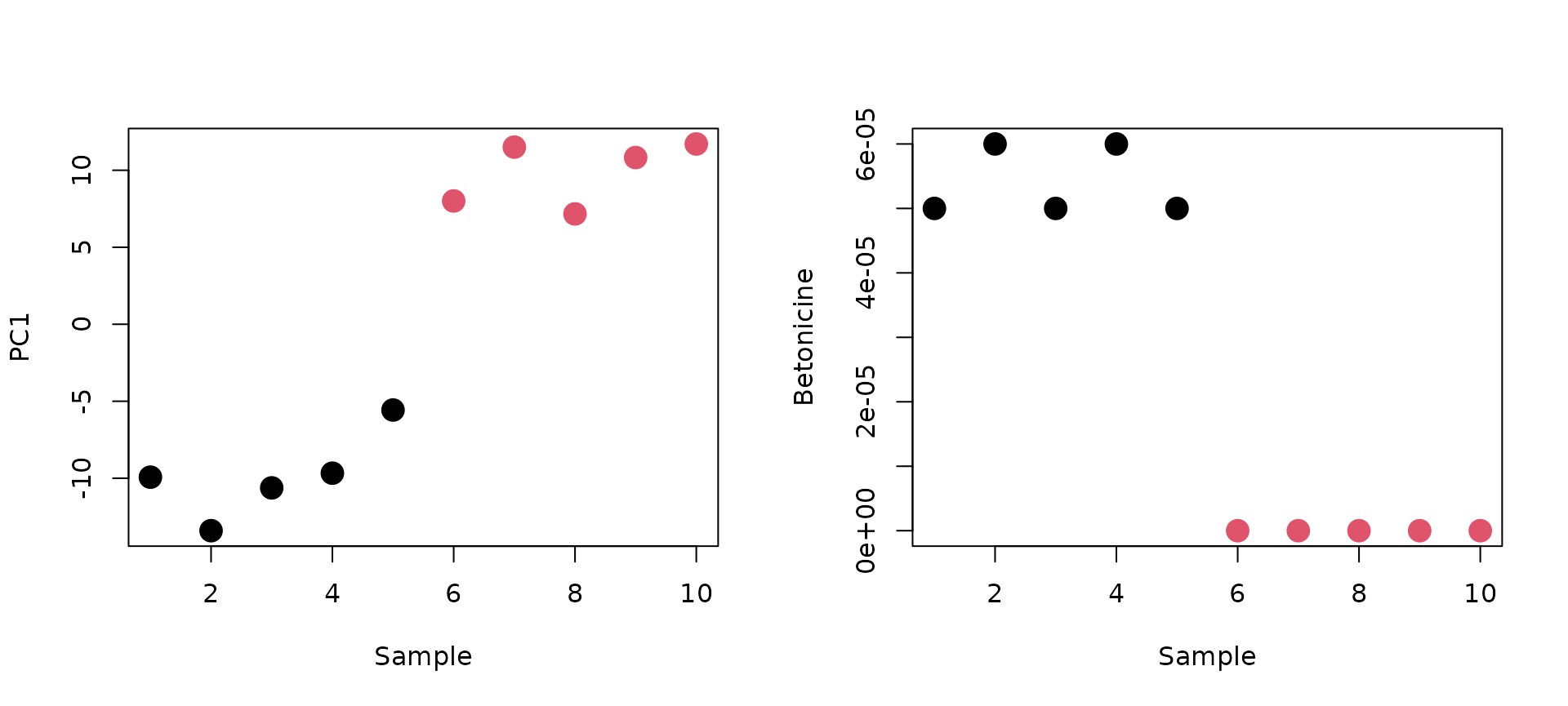
上図の左が第1主成分スコア,右がBetonicineである(横軸はサンプル番号).こちらは主成分負荷量(相関係数)の値が-0.980であり負に非常に高い値を示すことから分かるように,お互いに逆の傾向を示すことが確認できる.